It’s well known that SHA-1 is no longer considered a secure cryptographic hash function. Researchers now believe that finding a hash collision (two values that result in the same value when SHA-1 is applied) is inevitable and likely to happen in a matter of months. This poses a potential threat to trust on the web, as many websites use certificates that are digitally signed with algorithms that rely on SHA-1. Luckily for everyone, finding a hash collision is not enough to forge a digital certificate and break the trust model of the Internet.

We’ll explore how hash collisions have been used to forge digital signatures in the past. We’ll also discuss how certificate authorities can make this significantly harder for attackers in the future by including randomness in certificate serial numbers.

Digital signatures are the bedrock of trust

The Internet relies on trust. Whether it’s logging in to your bank or reading Reddit, HTTPS protects you by encrypting the data you exchange with a site and authenticating the site’s identity with a digital certificate. Browsers visually display the added security of HTTPS as a padlock in the address bar.

HTTPS can prove a site’s authenticity to a browser when a site owns a digital certificate that asserts the owner’s identity and hostname. Certificates are small files digitally signed by trusted third parties known as Certificate Authorities (CAs). For browsers, digital signatures are the definitive source of trust. If your browser trusts the CA and the digital signature on the certificate is correct, then the browser trusts the certificate. This system of identity is known as the public key infrastructure (PKI), something we’ve covered in detail in a previous post.

This system falls apart if digital signatures can no longer be trusted. If someone can create a certificate for cloudflare.com with a signature from a trusted CA, they can use it to impersonate the cloudflare.com website to visitors (given they can modify DNS).

A digital signature is a number cryptographically tied to a message with public key. Every digital signature requires a public-private key pair and a hash function. The hash function is used to take the message and replace it with a unique digest, the private key is used to sign, and the public key to verify signatures.

For example, to create an RSA signature, you take a hash of the message and encrypt that hash with your private key. Anyone can verify that signature both belongs to you and is valid for the associated message. Take the public key, decrypt the hash and compare it with the hash of the message. If it’s a match, the signature is correct. ECDSA is a more recent algorithm that gets the same job done.

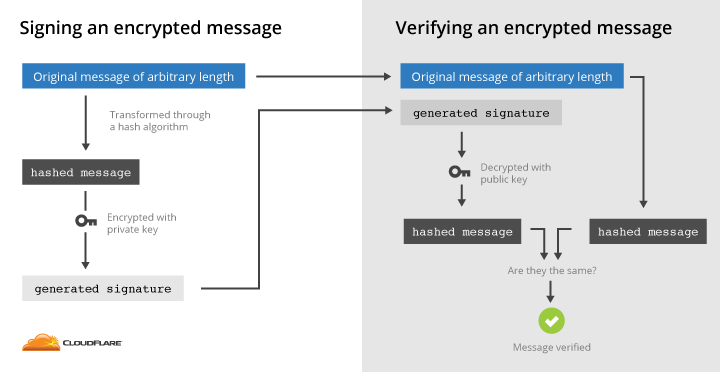
There are several ways of obtaining a digitally signed certificate for a website. The standard way is by purchasing a certificate from a certificate authority like GlobalSign or Comodo. CAs follow a set of rules about certificate issuance, governed by CA/Browser Forum’s Baseline Requirements.

Another way to get a certificate is to steal a CA’s private key. In addition to being potentially illegal, it is also very hard to do: CA private keys are usually kept in dedicated secure machines called Hardware Security Modules (HSM) designed to protect against key extraction.

A third more interesting way to obtain a certificate is to create a certificate that has the same hash as an existing trusted certificate. The signature from the trusted certificate can be added to the untrusted certificate, making it appear trusted.

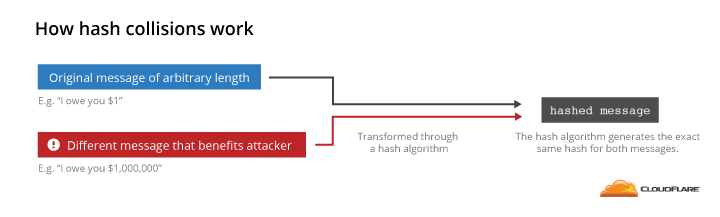
If you can find a message that has the same hash value as a signed message, then you can swap in your message and the signature will verify correctly. This can be used to trick anyone into thinking someone signed a message that they didn’t.

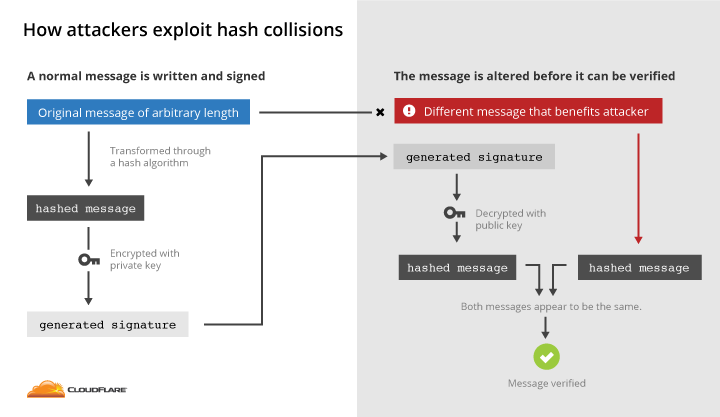
Cryptographic hash functions are designed to resist this sort of thing. They don’t always succeed.

Security properties of hash functions

Cryptographic hash functions are designed to satisfy three security properties:

• collision resistance
• second pre-image resistance
• pre-image resistance

Collision resistance here means are no known algorithms faster than brute force to find two values that hash to the same value. This is the strongest security requirement, and usually the first one to be broken.

A hash function has second pre-image resistance when, given a value and its hash, it is computationally infeasible to find a second value that hashes to the same value. On the surface, this would seem like the security property that protects digital signatures on certificates. However, as we’ll explore in the next section, it’s still possible to forge certificates signed with a second pre-image resistant hash.

Pre-image resistance means that given a hash, it’s computationally infeasible for an attacker to find a value that hashes to it. If you can find a pre-image, you can easily find a second pre-image or a collision.

In the next section, we’ll describe what happened the last time we used a cryptographic hash function without collision resistance for digital signatures.

Breaking MD5

MD5 is an incredibly popular cryptographic hash function; it also happens to be completely broken with respect to collision resistance. MD5 is still widely used, just not for digital signatures.

The first collision in MD5, discovered in 2004 by a group of Chinese researchers (PDF), used a lot of math and about an hour of computation by a supercomputer. Today, computing an MD5 collision takes only seconds on a laptop. This was cleverly demonstrated by Nat McHugh, who used the broken hash function MD5 to create two images with the same hash—in this case Barry White and James Brown (he later created a three-way collision with Jack Black).

Three images with the same MD5 hash:

You can verify this yourself via curl and md5:

$ curl -s https://blog.cloudflare.com/content/images/2015/08/white.jpg | md5
b69dd1fd1254868b6e0bb8ed9fe7ecad  
$ curl -s https://blog.cloudflare.com/content/images/2015/08/brown.jpg | md5
b69dd1fd1254868b6e0bb8ed9fe7ecad  
$ curl -s https://blog.cloudflare.com/content/images/2015/08/black.jpg | md5
b69dd1fd1254868b6e0bb8ed9fe7ecad  

Despite being relatively trivial to find an MD5 collision, it’s still not known how to perform a second-preimage attack on MD5. For example, given a digitally signed certificate, nobody has been able to create a second certificate with the same hash. Despite this, researchers created a certificate with the same signature as a certificate trusted by browsers.

The technique they used, a chosen-prefix attack, was originally proposed by Marc Stevens in his Master’s Thesis. It can be used to create a forged certificate as long as you can get a certificate authority to issue a certificate that starts with predictable values.

Chosen-prefix attacks

If you can find a collision, you can take two different values and append data to each so they hash to the same value. In the original MD5 collision attack, the researchers computed two messages M1 and M2 such that H(M1) = H(M2). Stevens extended this research to find a way to make two known values P1 and P2 collide by appending bytes. With prefixes P1 and P2, he was able to demonstrate how to find S1 and S2 so that H(P1|S1) = H(P2|S2).

This was enough to allow an attacker to create two certificates with the same hash. Let’s look at the approximate structure of a certificate:

• Serial number
• Validity period
• Domain name
• Public key
• X.509 extensions
• Signature

If the attacker knows every value before the domain, then they can take

P1 = Serial number | Validity period | real domain name  

and

P2 = Serial number | Validity period | forged domain name  

and apply the attack to get S1 and S2 that fit into the public key section. If the serial number and validity period can be predicted, a collision can be found using the following steps:

1. Guess when the certificate will be issued;
2. Predict the serial number for certificates issued in that time period; and
3. Compute matching prefixes for several guesses covering the expected serial numbers and issuance dates

The attack precomputes collisions for the choices for each of these values, where one guess has a domain name that is under the requester’s control (e.g. for attacker.com) and one for the target domain (e.g. google.com). Once those are computed and you can convince a CA to issue a certificate at correct time for the valid values, you can transpose that valid signature onto a malicious certificate.

Forging MD5 certificates in practice

In 2008, several researchers (including Marc Stevens) used the chosen prefix collision techniques to forge a certificate authority trusted by browsers. This proof of concept was presented at the Chaos Communication Congress in 2008 and required only a few days of computation.

In 2012, a piece of malware called Flame was discovered. Flame was able infect computers by hijacking Microsoft’s Windows Update mechanism. At the time, Windows Update validated updates by checking code signatures using certificates signed by Microsoft using a MD5-based signature. The authors of Flame used a forged Microsoft certificate. According to an analysis of this certificate, it was likely the chosen-prefix technique was used to create Flame’s forged certificate.

Forbes declared this the most worrisome security discovery of 2012 since it demonstrated it was feasible for attackers to forge any website’s certificate using an MD5 hash collision when the client trusts MD5-signed certificates.

SHA-1 vs MD5

SHA-1 is supposedly more secure than MD5 for use in digital signatures. The National Security Agency published SHA-1 (SHA stands for Secure Hash Algorithm) in 1995 as a standard for cryptographically secure hashing. Designed to be collision resistant up to 2⁸⁰ bits, SHA-1 has had a long and useful life, and a collision has not been published as of this blog post. Even though a collision has never been published, several theoretical attacks (the first in 2005, improved in 2012) indicate that SHA-1 is not as secure as its bit length implies. The latest research suggests that its collision resistance is at best 2⁶⁵ — within the realm of feasibility for some governments. In fact, researchers published a freestart collision (a precursor to a full collision) for SHA-1 earlier this year.

CC BY-SA 2.0

Academic cryptanalysts are like sharks. If there’s blood in the water, they swarm. It took nine years to get from the first published weakness in MD5 (1996) to a hash collision (2005), and then another three years to forge a trusted digital signature (2008). They might be slow, but they’re relentless.

Attacks always improve and computers get more powerful. It was nine years from first weakness to hash collision in MD5; it’s been ten years for SHA-1. If history is any guide, a public collision for SHA-1 could be published at any moment, with chosen-prefix collisions arriving soon after.

Preventing chosen-prefix attacks by requiring serial number entropy

One way to improve the security of digital signatures against a chosen-prefix attack is to make the prefix less predictable.

As described above, the chosen prefix attack requires the attacker to predict both the serial number and the validity period. Certificates used on the web have serial numbers up to 160 bits long. Requiring CAs to make the serial number unpredictable instead of sequential, it is possible to make the chosen-prefix attack significantly more expensive.

For example, if a CA ensures the serial number contains 20 bits of entropy, then the attacker will need to compute 2²⁰ chosen-prefixes in order to guess the serial number correctly.

This makes the attack over a million times more difficult.

Computing a SHA-1 collision might be feasible in 2016, and there’s a chance that chosen-prefix attacks also become feasible. Nevertheless, choosing partially randomized serial can make certificate forgery significantly more difficult for attackers. Barring a breakthrough in hash collision techniques, it’s unlikely we’ll see a certificate collision for long time.

Conclusion

The SHA-1 hash function, widely used for everything from file integrity to digital signatures, is at the end of its useful life. Some browsers even show security warnings when websites use certificates signed using a SHA-1 based digital signature. A hash collision in SHA-1 is bad, but it’s not what matters for web security. Digital signature forgery is more problematic for trust on the Web. Requiring CAs to randomize serial numbers will significantly increase the cost of such forgeries, allowing potentially weak algorithms like SHA-1 to be useful for longer. This is why we make it mandatory for CAs to use serial numbers that include at least 20 bytes of entropy in our proposal to the CA/B For for Legacy Verified (LV) SHA-1 certificates.

Via Cloudflare.com