Yesterday a new vulnerability has been announced in OpenSSL/LibreSSL. A padding oracle in CBC mode decryption, to be precise. Just like Lucky13. Actually, it’s in the code that fixes Lucky13.

It was found by Juraj Somorovsky using a tool he developed called TLS-Attacker. Like in the “old days”, it has no name except CVE-2016-2107. (I call it LuckyNegative20¹)

It’s a wonderful example of a padding oracle in constant time code, so we’ll dive deep into it. But first, two quick background paragraphs. If you already know all about Lucky13 and how it’s mitigated in OpenSSL jump to “Off by 20” for the hot and new.

If, before reading, you want to check that your server is safe, you can do it with this one-click online test.

TLS, CBC, and Mac-then-Encrypt

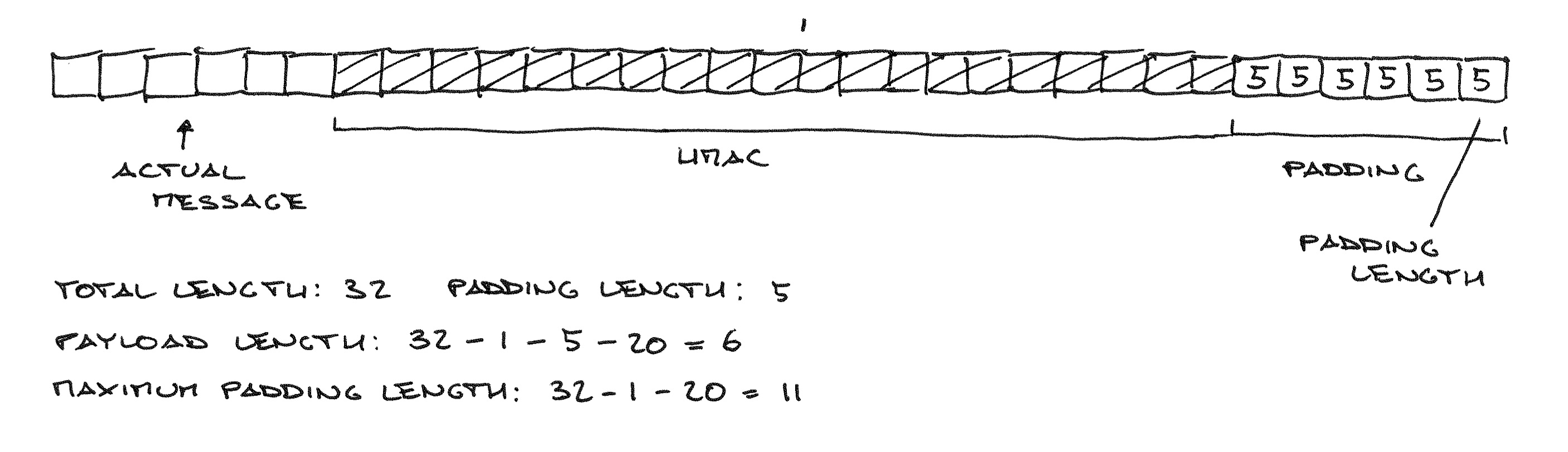
Very long story short, the CBC cipher suites in TLS have a design flaw: they first compute the HMAC of the plaintext, then encrypt plaintext || HMAC || padding || padding length using CBC mode. The receiving end is then left with the uncomfortable task of decrypting the message and checking HMAC and padding without revealing the padding length in any way. If they do, we call that a padding oracle, and a MitM can use it to learn the value of the last byte of any block, and by iteration often the entire message.

Click to enlarge the diagrams.

In other words, the CBC mode cipher suites are doomed by The Cryptographic Doom Principle. Sadly though, they are the only “safe” cipher suites to use with TLS prior to version 1.2, and they account for 26% of connections to the CloudFlare edge, so attacks against them like this one are still very relevant.

My colleague Nick Sullivan explained CBC padding oracles and their history in much more detail on this very blog. If you didn’t understand my coarse summary, please take the time to read his post as it’s needed to understand what goes wrong next.

Constant time programming crash course

The “solution” for the problem of leaking information about the padding length value is to write the entire HMAC and padding check code to run in perfectly constant time. What I once heard Daniel J. Bernstein call “binding your hands behind your back and seeing what you can do with just your nose”. As you might imagine it’s not easy.

The idea is that you can’t use ifs. So instead you store the results of your checks by doing bitwise ANDs with a result variable which you set to 1 before you begin, and at which you only look at the end of the entire operation. If any of the checks returned 0, then the result will be 0, otherwise it will be 1. This way the attacker only learns “everything including padding and HMAC is good” or “nope”.

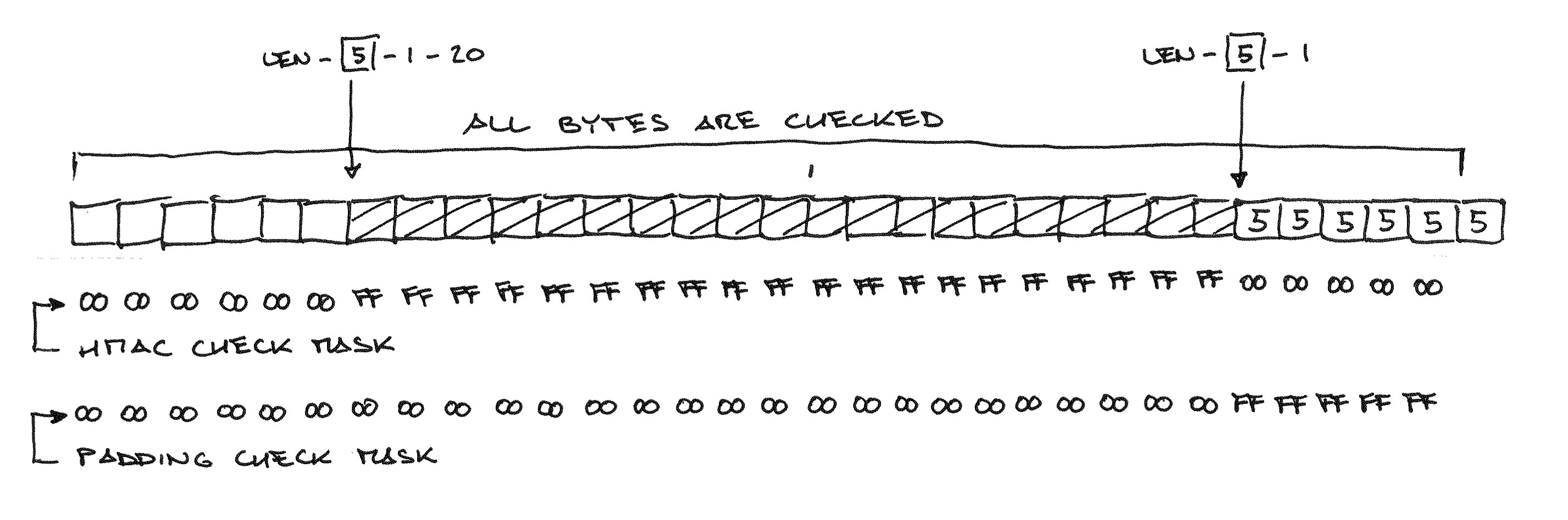
Not only that, but loop iterations can only depend on public data: if for example the message is 32 bytes long then the padding can be at most 32-1-20=11 bytes, so you have to check 20 (HMAC-SHA1) + 11 bytes. To ignore the bytes you don’t actually have to check, you use a mask: a value generated with constant time operations that will be 0xff when the bytes are supposed to match and 0x00 when they are not. By ANDing the mask to the bitwise difference you get a value which is 0 when the values either match, or are not supposed to match.

This technique is crucial to this vulnerability, as it’s exactly its constant time, no-complaints nature that made the mistake possible.

The OpenSSL checking code was written after the discovery of Lucky13, and Adam Langley wrote a long blog post explaining how the generic version works. I glossed over many details here, in particular the incredible pain that is generating the HMAC of a variable-length message in constant time (which is where Lucky13 and Lucky Microseconds happened), so go read his incredible write-up to learn more.

Off by 20

Like any respectable vulnerability analysis, let’s start with the patch. We’ll focus on the SHA1 part for simplicity, but the SHA256 one is exactly the same.

The patch for LuckyMinus20 is one line in the OpenSSL function that performs AES-CBC decryption and checks HMAC and padding. All it is doing is flagging the check as failed if the padding length value is higher than the maximum it could possibly be.

              pad = plaintext[len - 1];
              maxpad = len - (SHA_DIGEST_LENGTH + 1);
              maxpad |= (255 - maxpad) >> (sizeof(maxpad) * 8 - 8);
              maxpad &= 255;

 +            ret &= constant_time_ge(maxpad, pad);
 +

This patch points straight at how to trigger the vulnerability, since it can’t have any side effect: it’s constant time code after all! It means that if we do what the patch is there to detect—send a padding length byte higher than maxpad—we can sometimes pass the HMAC/padding check (!!), and use that fact as an oracle.

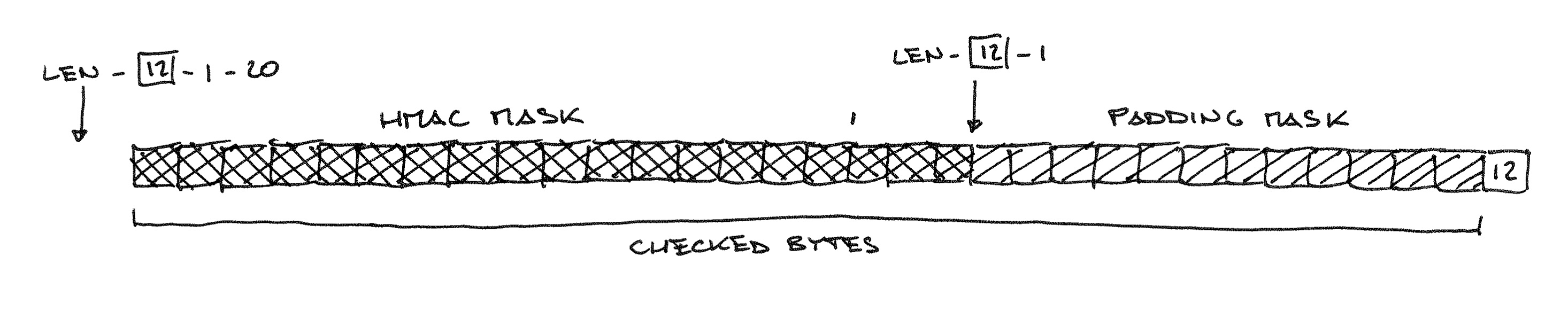
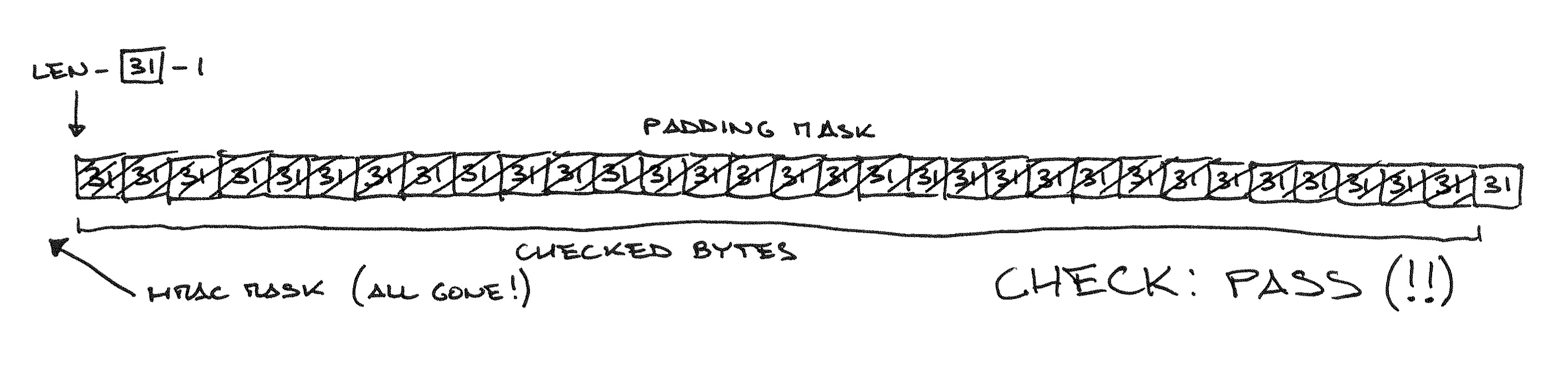
maxpad is easily calculated: length of the plaintext, minus one byte of payload length, minus 20 bytes of HMAC-SHA1 (SHA_DIGEST_LENGTH), capped at 255. It’s a public value since it only depends on the encrypted data length. It’s also involved in deciding how many times to loop the HMAC/padding check, as we don’t want to go out of the bounds of the message buffer or waste time checking message bytes that couldn’t possibly be padding/HMAC.

So, how could pad > maxpad allow us pass the HMAC check fraudulently?

Let’s go back to our masks, this time thinking what happens if we send:

pad = maxpad + 1 = (len - 20 - 1) + 1 = (32 - 20 - 1) + 1 = 12  

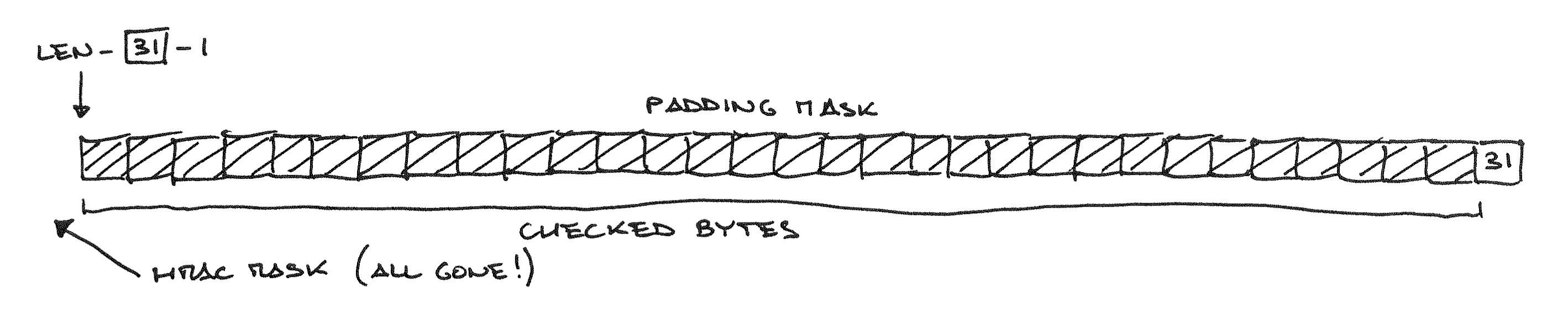
Uh oh. What happened there!? One byte of the HMAC checking mask fell out of the range we are actually checking! Nothing crashes because this is constant time code and it must tolerate these cases without any external hint. So, what if we push a little further…

There. The HMAC mask is now 0 for all checking loop iterations, so we don’t have to worry about having a valid signature at all anymore, and we’ll pass the MAC/padding check unconditionally if all bytes in the message are valid padding bytes—that is, equal to the padding length byte.

I like to box and label these kinds of “cryptanalytic functions” and call them capabilities. Here’s our capability:

We can discover if a message is made entirely of bytes with value n, where n >= maxpad + 20 by sending it to the server and observing an error different from BAD_MAC. This can only work with messages shorter than 256-20=236 bytes, as pad can be at most 255, being a 8-bit value.

NOTE: A MitM is not able to distinguish the different error codes since they are encrypted alerts, but since each error code takes a different code path the timing difference could be observed. Also, other side-channels might exist that I’m missing at the moment, since there’s no protection in place to make different alerts truly indistinguishable.

We can use this capability as an oracle.

In other words, the entire trick is making the computed payload length “negative” by at least DIGEST_LENGTH so that the computed position of the HMAC mask is fully “outside” the message and the MAC ends up not being checked at all.

By the way, the fact that the affected function is called aesni_cbc_hmac_sha1_cipher explains why only servers with AES-NI instructions are vulnerable.

You can find a standalone, simplified version of the vulnerable function here, if you want to play with the debugger yourself.

From there to decryption

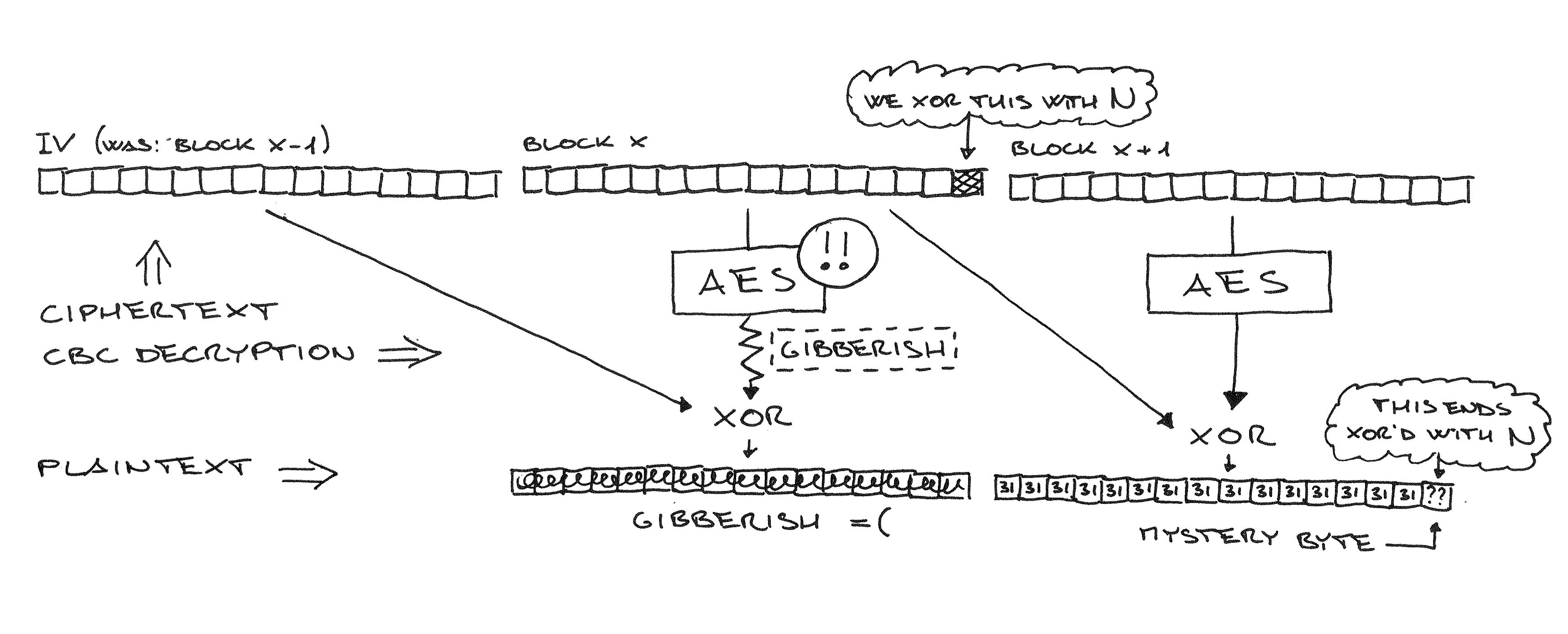
Ok, we have a “capability”. But how do we go from there to decryption? The “classic” way involves focusing on one byte that we don’t know, preceded by bytes we control (in this case, a string of 31). We then guess the unknown byte by XOR’ing the corresponding ciphertext byte in the previous block with a value n. We do this for many n. When the server replies “check passed”, we know that the mystery byte is 31 XOR n.

Remember that this is CBC mode, so we can cut out any consecutive sequence of blocks and present it as its own ciphertext, and values XOR’d to a given ciphertext byte end up XOR’d to the corresponding plaintext byte in the next block. The diagram below should make this clearer.

In this scenario, we inject JavaScript in a plain-HTTP page the user has loaded in a different tab and send as many AJAX requests as we want to our target domain. Usually we use the GET path as the known controlled bytes and the headers as the decryption target.

However, this approach doesn’t work in this case because we need two blocks of consecutive equal plaintext bytes, and if we touch the ciphertext in block x to help decrypt block x + 1, we mangle the plaintext of block x irreparably.

I’d like you to pause for a minute to realize that this is at all possible only because we:

1. Allow unauthenticated (plain-HTTP) websites—and so any MitM—to run code on our machines.

2. Allow JavaScript to send requests to third-party origins (i.e. other websites) which carry our private cookies. Incidentally, this is also what enables CSRF.

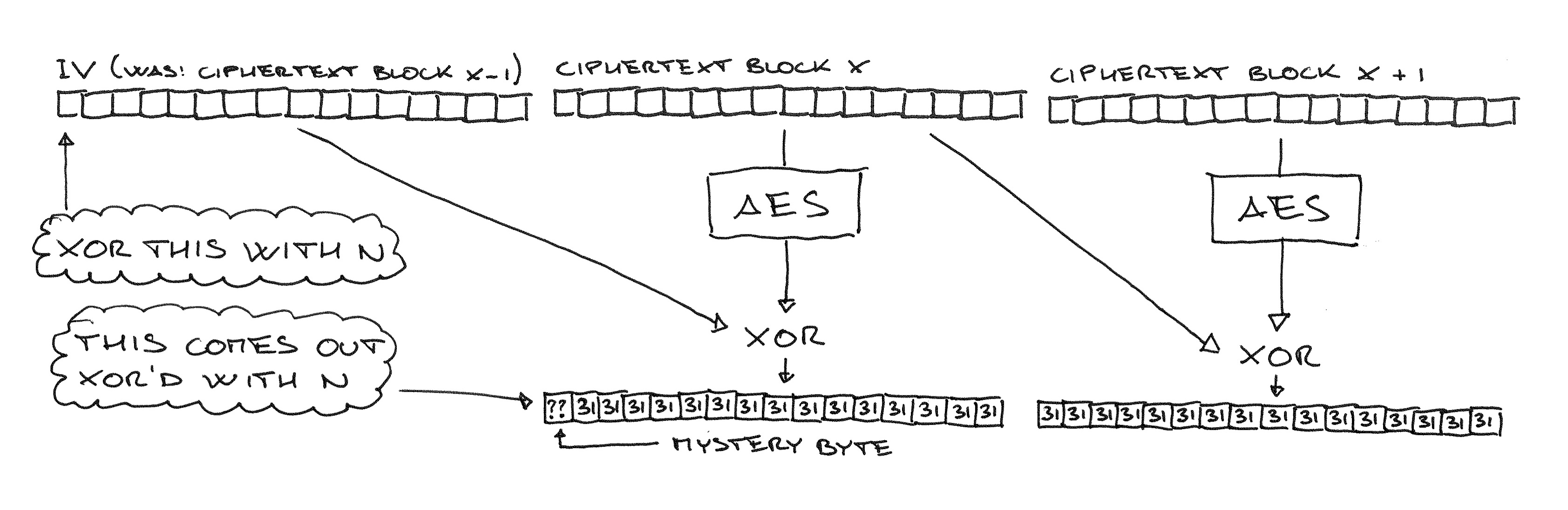
Back to our oracle, we can make it work the other way around: we align an unknown byte at the beginning of two blocks made of 31 (which we can send as POST body) and we XOR our n values with the first byte in the IV. Again, when the MAC check passes, we know that the target byte is 31 XOR n.

We iterate this process, moving all bytes one position to the right (for example by making the POST path one character longer), and XOR’ing the first byte of the IV with our n guesses, and the second byte with the number we now know will turn it into a 31.

And so on and so forth. This gets us to decrypt any 16 bytes that consistently appear just before a sequence of at least 31 attacker-controlled bytes and after a string of attacker-controlled length (for alignment).

It might be possible to extend the decryption to all blocks preceding the two controlled ones by carefully pausing the client request and using the early feedback, but I’m not sure it works. (Chances of me being wrong on full decryption capabilities are high, considering that an OpenSSL team member said they are not aware of such a technique.)

But no further

One might think that since this boils down to a MAC check bypass, we might use it to inject unauthenticated messages into the connection. However, since we rely on making pad higher than maxpad + DIGEST_LENGTH, we can’t avoid making the payload length (totlen - 1 - DIGEST_LENGTH - pad) negative.

pad > maxpad + DIGEST_LENGTH = (totlen - DIGEST_LENGTH - 1) + DIGEST_LENGTH = totlen - 1 > totlen - 1 - DIGEST_LENGTH  
0 > totlen - 1 - DIGEST_LENGTH - pad = payload_len  

Since length is stored as an unsigned integer, when it goes negative it wraps around to a very high number and triggers the “payload too long” error, which kills the connection. Too bad… Good. I meant good 🙂

This means, by the way, that successful attempts to exploit or test this vulnerability show up in OpenSSL logs as

SSL routines:SSL3_GET_RECORD:data length too long:s3_pkt.c:  

Testing for the vulnerability

Detecting a vulnerable server is as easy as sending an encrypted message which decrypts to AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA, and checking if the TLS alert is DATA_LENGTH_TOO_LONG (vulnerable) or BAD_RECORD_MAC (not vulnerable).

It works because A is 65, which is more than 32 – 1.

There’s a simple implementation at https://github.com/FiloSottile/CVE-2016-2107 and an online version at https://filippo.io/CVE-2016-2107/

Conclusion

To sum up the impact: when the connection uses AES-CBC (for example because the server or the client don’t support TLS 1.2 yet) and the server’s processor supports AES-NI, a skilled MitM attacker can recover at least 16 bytes of anything it can get the client to send repeatedly just before attacker-controlled data (like HTTP Cookies, using JavaScript cross-origin requests).

A more skilled attacker than me might also be able to decrypt more than 16 bytes, but no one has shown that it’s possible yet.

All CloudFlare websites are protected from this vulnerability. Any website which had enabled our TLS 1.2-only feature was never affected. Connections from the CloudFlare edge to origins use TLS 1.2 and AES-GCM if the server supports it, so are safe in that case. Customers supporting only AES-CBC should upgrade as soon as possible.

In closing, the cryptographic development community has shown that writing secure constant-time MtE decryption code is extremely difficult to do. We can keep patching this code, but the safer thing to do is to move to cryptographic primitives like AEAD that are designed not to require constant time acrobatics. Eventually, TLS 1.2 adoption will be high enough to give CBC the RC4 treatment. But we are not there yet.

Are you crazy enough that analyzing a padding oracle in a complex crypto protocol sounds exciting to you? We are hiring in London, San Francisco, Austin and Singapore, including cryptography roles.

Thanks to Anna Bernardi who helped with the analysis and the painful process of reading OpenSSL code. Thanks (in no particular order) to Nick Sullivan, Ryan Hodson, Evan Johnson, Joshua A. Kroll, John Graham-Cumming and Alessandro Ghedini for their help with this write-up.

Via Cloudflare.com